Next: Elastic Collisions Up: VM_Exat98A Previous: X-Ray Yields

Kinetic Energy Distribution in Excited States

The evolution of the kinetic energy distribution during the atomic cascade is very important because many collisional processes are energy dependent (Table 1). In muonic atoms, it determines the initial energy distribution in the ground state, which influences the diffusion of $\mu$ -atoms [41,42,43] and muon catalyzed fusion [44,45]. A large fraction of the atoms is not thermalized² during the atomic cascade, as it follows from the cascade calculation demonstrated in Fig.3b.

**Figure 4:** (a) The kinetic energy distribution at the instant of the $3P\to 1S$ transition in muonic hydrogen at 15 bar, (b) the corresponding Doppler broadening of the $K_{\beta }$ line and (c) the cumulative energy distribution .
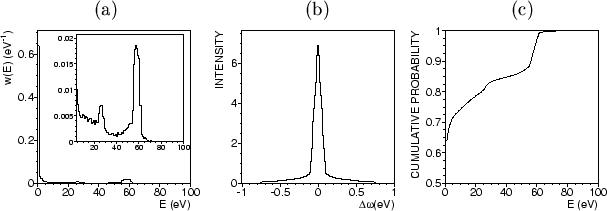
$\begin{figure} \mbox{\hspace{20mm} (a)\hspace{40mm} (b)\hspace{40mm}(c)} \\ [-0.... ...pK3G15X.eps}}%\mbox{\epsfxsize =45mm\epsffile {mupK3G15CE.eps}} } \end{figure}$

The kinetic energy distribution in the atomic cascade can be studied with different methods. Direct probes which are model independent are based on the measurements of the Doppler broadening of the X-ray lines in $\mu p$ and $\pi ^-p$ and the -TOF spectra in the reaction $\pi^-p\to\pi^0+n$ . Given the kinetic energy distribution at the instant of the radiative transition, the Doppler broadening of the X-ray line $g(\Delta\omega)$ has the form:

$\displaystyle g(\Delta \omega)$

$\textstyle =$

$\displaystyle \frac{1}{2\xi} \int_{(\Delta \omega/\xi)^2}^{\infty} \frac{w(E)}{\sqrt{E}} dE \ , \quad \xi = \frac{\omega_0}{c} \sqrt{\frac{2}{M}}$

(4)

where $\omega_0$ is the X-ray energy in the atomic rest frame and

is the mass of the atom. A straightforward inversion of the transformation (4) gives the cumulative energy distribution

$\displaystyle W(E) \stackrel{def}{=} \int_{0}^{E} w(E') dE'$

$\textstyle =$

$\displaystyle 2 \int_{_{0}}^{^{\xi\sqrt{E}}} g(x) dx - 2 \xi\sqrt{E} g(\xi\sqrt{E}) \quad .$

(5)

Figure 4 shows an example of the calculated distributions for the $K_{\beta }$ -transition in $\mu p$ atoms at 15 bar which features characteristic peaks in the high-energy component resulting from the Coulomb de-excitation discussed in Sec. 6. The Doppler broadening of the neutron TOF spectra from the reaction $(\pi^-p)\to\pi^0+n$ is related to the kinetic energy distribution in a similar way (see [46,47,48]). A good knowledge of the kinetic energy distribution is essential for precise measurements of the $(\pi^-p)_{1S}$ nuclear width [49]. For example, the kinetic energy $T=0.5\;$ eV corresponds to a Doppler broadening of the $K_{\beta }$ line $\delta\Gamma=0.1\;$ eV which is about 10% of the nuclear width $\Gamma_{1S}=1\;$ eV.

Indirect methods of probing the kinetic energy distribution rely on models of the kinetics. In particular, the first evidence for epithermal muonic atoms was found in muon catalyzed fusion (see [45] and references therein). Important results on the initial kinetic energy distribution in the ground state were obtained from the diffusion of $\mu p$ and $\mu d$ atoms at low density [41,42,43]; they allow one to determine the energy distribution in excited states using cascade models as discussed in [4,43]. Indirect methods exploiting energy dependent processes, like the muon transfer in excited states [26,50,51], were used for the estimates of the average energy in excited states, however, they are not sensitive to the details of the energy distributions.

Next: Elastic Collisions Up: VM_Exat98A Previous: X-Ray Yields

Valeri Markushin
2000-08-05