next up previous
Next: Coulomb De-excitation Up: VM_Exat98A Previous: Kinetic Energy Distribution in

Elastic Collisions

The elastic collisions, where the principal quantum number of the exotic atom is not changed, play two important roles in the atomic cascade. First, the Stark mixing is nothing but the elastic scattering as long as only the rates of transitions between the $l$-sublevels of the same $n$ are concerned. Second, the energy losses in elastic collisions lead to the deceleration of the epithermal exotic atoms.

The basic features of the elastic scattering can be explained in the semiclassical approximation [23]. The motion of the $\mu p$ atom with the parabolic quantum numbers $(n_1,n_2,m)$ in the electric field of a hydrogen atom is described by the effective potential3

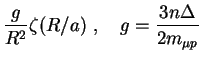$\displaystyle V(R)$ $\textstyle =$ $\displaystyle \frac{g}{R^2} \zeta(R/a) \ , \quad g = \frac{3n\Delta}{2m_{\mu p}}$ (6)

where $\Delta=(n_1-n_2)$, $m_{\mu p}$ is the $\mu p$ reduced mass, $\zeta(r)=(1+2r+2r^2){\rm e}^{-2r}$ is the electron screening factor, $a$ is the electron Bohr radius. Neglecting the electron screening, this corresponds to the well known $R^{-2}$ potential with a large dimensionless coupling constant $2Mg=\frac{3}{2}n\Delta M/m_{\mu p}\sim Mn^2/m_{\mu p}\gg 1$ ($M$ is the reduced mass of the $\mu p+p$ system). The $R^{-2}$ behaviour leads to the $E^{-1}$ dependence of the elastic cross section. In the limit $2Mg\gg 1$, many partial waves contribute to the scattering, and the differential cross section can be approximated by the classical result ($g>0$):
$\displaystyle \frac{d\sigma(E,\theta)}{d\Omega}$ $\textstyle =$ $\displaystyle \frac{\pi g}{E} \; w(\theta)$ (7)
$\displaystyle w(\theta)$ $\textstyle =$ $\displaystyle \frac{\pi(\pi-\theta)}{(2\pi-\theta)^2\; \theta^2 \sin{\theta} } \approx \frac{1}{32 \sin^3{\theta/2}}$ (8)

The average coupling constant for given $n$ is $g=(n^2-1)/2m_{\mu p}$. The cross section (7,8) has an unphysical singularity at $\theta\to 0$ which must be regularized by taking the electron screening into account.

A semiclassical model of the Stark mixing was developed in [1] and used with some variations and refinements in [6,7,8,10]. In this model, the exotic atom moves along a straight line trajectory with a constant velocity through the electric field of a hydrogen atom, and the Stark transitions induced by this electric field are calculated. Instead of straight line trajectories the classical trajectories can be used as in [28]. The characteristic scale of the Stark mixing cross section is determined by the electron screening of the proton electric field, i.e. by the size of the hydrogen atom which makes Stark mixing the fastest collision process in the atomic cascade, see Figs. 2.

Recently the problem of the elastic scattering of exotic atoms in excited states was treated in a quantum mechanical framework using the adiabatic expansion [9,11,15], the calculation being done in a single-channel adiabatic approximation. The results show fair agreement with the semiclassical calculations [14] for the collision energies $E>1\;$eV. A detailed discussion of the Stark collisions, including the relative role of transitions with different $\Delta l=l_f-l_i$ can be found in [11]. It would be desirable to extend the quantum mechanical model of the elastic collisions by including the effects of the shift and width of the $nS$ states as well as the coupling between different adiabatic terms.

The elastic scattering leads to the deceleration of exotic atoms if the kinetic energy is larger than the target temperature. The effective deceleration rate for the $\mu p+p$ collisions is defined by the transport cross section:

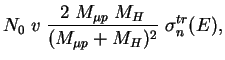$\displaystyle \lambda_n^{dec}(E)$ $\textstyle =$ $\displaystyle N_0\; v\; \frac{2\;M_{\mu p}\;M_H}{(M_{\mu p}+M_H)^2}\;\sigma_n^{tr}(E) ,$ (9)
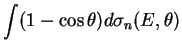$\displaystyle \sigma_n^{tr}(E)$ $\textstyle =$ $\displaystyle \int (1-\cos\theta) d\sigma_n(E,\theta)$ (10)

where $v$ is the atomic velocity, $M_{\mu p}$ and $M_H$ are the $\mu p$ and hydrogen masses correspondingly. Using the classical result (7,8) one gets the following estimation4of the transport cross section:
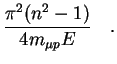$\displaystyle \sigma_n^{tr}(E)$ $\textstyle \approx$ $\displaystyle \frac{\pi^2(n^2-1)}{4m_{\mu p}E} \quad .$ (11)

The deceleration rate (Fig. 2) is a crude measure of the slowing down; in general one uses the differential cross sections in detailed kinetics calculations. The first estimation of the deceleration rates was done in [12], semiclassical calculations were done in [13,14], and quantum mechanical calculations in [9,11,15].

next up previous
Next: Coulomb De-excitation Up: VM_Exat98A Previous: Kinetic Energy Distribution in
Valeri Markushin
2000-08-05