Next: Kinetic Energy Distribution in Up: VM_Exat98A Previous: Cascade Mechanisms

X-Ray Yields

Since the rates of the radiative transitions are well known, the competition between the radiative and collisional processes can be used for testing the collisional de-excitation rates by measuring the X-ray yields at various densities. The most suitable system for this study is the muonic hydrogen where the X-ray yields are not suppressed by absorption during the cascade. Another convenient factor is that the rates of the Auger de-excitation, which is the main collisional process, have a weak energy dependence, therefore they are not strongly affected by uncertainties in the kinetic energy distribution. The main features of the density dependence of the yields of the -lines were already fairly well explained by the MCM [7,8]. Figure 3a shows the experimental data in comparison with the recent calculations [4] that include, in addition to the Auger de-excitation, the Coulomb transitions.

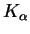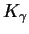**Figure:** (a) The density dependence of the $K_{\alpha }$ , $K_{\beta }$ , and $K_{\gamma }$ yields in muonic hydrogen. The theoretical curves are from [4], the experimental data from [32,33,34,35,36,37,38,39]. (b) The density dependence of the high-energy components ( 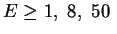$E\geq 1,\ 8,\ 50\;$ eV) in the $\mu p$ ground state after the atomic cascade calculated in the model [4] with the Coulomb rates scaled by a factor 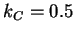[29].
$\begin{figure} \mbox{\hspace{25mm} (a) \hspace{60mm} (b)}\\ [-0.5\baselineskip] ... ...XyldAllBW.eps}}%\mbox{\epsfysize =65mm\epsffile {mupHighE.eps}} } \end{figure}$

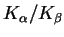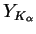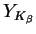The relative role of the collisional processes can be illustrated by the following simplified calculation of the density dependence of the $K_{\alpha}/K_{\beta}$ ratio using the method suggested in [40]. The yields $Y_{K_{\alpha}}$ and $Y_{K_{\beta}}$ are given by the balance equations:

$\displaystyle Y_{K_{\alpha}}$	$\textstyle \approx$	$\displaystyle p_{2} \; \approx \; p_{3} \; \frac{ \lambda^{\gamma}_{3\to 2}+ \phi(\lambda^{Auger}_{3\to 2}+\lambda^{Coulomb}_{3\to 2})} {\lambda^{tot}_3}$	(1)
$\displaystyle Y_{K_{\beta}}$	$\textstyle =$	$\displaystyle p_{3} \; \frac{\lambda^{\gamma}_{3\to 1}}{\lambda^{tot}_3} \ , \q... ...da^{\gamma}_{3\to 1} +\phi(\lambda^{Auger}_{3\to 2}+\lambda^{Coulomb}_{3\to 2})$	(2)

where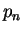

are the populations of the atomic states

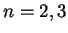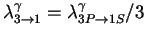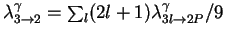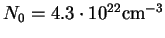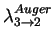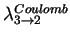, $\lambda^{\gamma}_{3\to 1}=\lambda^{\gamma}_{3P\to 1S}/3$ and $\lambda^{\gamma}_{3\to 2}=\sum_l(2l+1)\lambda^{\gamma}_{3l\to 2P}/9$ are the effective rates of the radiative transitions, $\phi$ is the hydrogen density in units of liquid hydrogen density $N_0=4.3\cdot 10^{22}\mbox{\rm cm}^{-3}$ (LHD), $\lambda^{Auger}_{3\to 2}$ and $\lambda^{Coulomb}_{3\to 2}$ are the rates of the Auger and Coulomb transitions normalized to LHD. 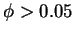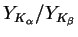Equations (1,2) are valid at $\phi>0.05$ and give the following dependence of the ratio $Y_{K_{\alpha}}/Y_{K_{\beta}}$ on the density:

$\displaystyle \frac{Y_{K_{\alpha}}}{Y_{K_{\beta}}}$

$\textstyle =$

$\displaystyle \frac{\lambda^{\gamma}_{3\to 2}}{\lambda^{\gamma}_{3\to 1}} + \fr... ... \left( 1+ \frac{\lambda^{Coulomb}_{3\to 2}} {\lambda^{Auger}_{3\to 2}} \right)$

(3)

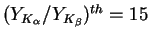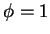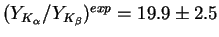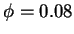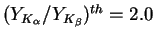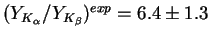If one neglects the Coulomb de-excitation, then Eq. (3) gives $(Y_{K_{\alpha}}/Y_{K_{\beta}})^{th}=15$ at $\phi=1$ which is slightly below the corresponding experimental ratio $(Y_{K_{\alpha}}/Y_{K_{\beta}})^{exp}=19.9\pm 2.5$ [38]. At $\phi=0.08$ the difference is larger: $(Y_{K_{\alpha}}/Y_{K_{\beta}})^{th}=2.0$ and $(Y_{K_{\alpha}}/Y_{K_{\beta}})^{exp}=6.4\pm 1.3$ . With the Coulomb transitions taken into account the theoretical ratio gets closer to the experimental values as discussed in [38,31]. This observation can be considered as evidence that some mechanisms in addition to the Auger effect, like the Coulomb transitions, are needed for a better description of the X-ray yields.

Next: Kinetic Energy Distribution in Up: VM_Exat98A Previous: Cascade Mechanisms

Valeri Markushin
2000-08-05