Appendix 2: Determination of the Kinetic Energy Distribution from the Doppler Broadening of the n-ToF and X-Ray Lines.

Let

be the normalized kinetic energy distribution of the exotic atom, then the cumulative energy distribution

is defined by the formula

$\displaystyle W(E)$

$\textstyle =$

$\displaystyle \int_{0}^{E} w(E') dE'$

(33)

$\displaystyle W(E_{max})$

$\textstyle =$

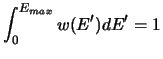$\displaystyle \int_{0}^{E_{max}} w(E') dE' = 1$

(34)

The neutron time of flight corresponding to the reaction $(\pi^-p)_{at}\to \pi^0+n$ at rest is

where

is the neutron flight path and $v_0=0.894\;$ cm/ns is the neutron velocity. The Doppler broadening of the neutron time-of-flight spectrum $f(\Delta t)$ , where $\Delta t = (t - t_0)$ is the difference between the measured time

and

, is related to the kinetic energy distribution

$\begin{displaymath} f(\Delta t)=\frac{1}{2\xi }\int _{(\Delta t/\xi )^{2}}^{E_{max}}\frac{w(E)}{\sqrt{E}}dE \end{displaymath}$

(35)

$\begin{displaymath} \xi =t_{0}\frac{c}{v_{0}}\sqrt{\frac{2}{M}} \end{displaymath}$

(36)

Given the Doppler profile $f(\Delta t)$ , one can determine the cumulative energy distribution

using the following formula which is derived straightforwardly from Eqs. (37-40):

$\begin{displaymath} W(E)=2\int ^{\xi \sqrt{E}}_{0}f(\tau )d\tau -2\xi \sqrt{E}f(\xi \sqrt{E}) \end{displaymath}$

(37)

Equation (41) can be used for the determination of the kinetic energy distribution from the measured neutron ToF spectrum in a model independent way as illustrated in Figs. 11, 12 and 13.

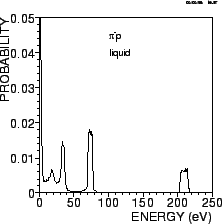
$\resizebox* {0.4\textwidth}{0.2\textheight}{\includegraphics{wae_pip_liq.epsi}}$

Figure 11: The calculated kinetic energy distribution of the $\pi ^{-}p$ atom at the instant of strong interaction in liquid hydrogen.

The theoretical kinetic energy distribution shown in Fig 11 corresponds to the n-ToF distribution plotted in Fig. 12. Applying Eq. (41) to the Monte Carlo generated spectrum $f(\Delta t)$ with $10^{5}$ events we obtain perfect reconstruction of the original kinetic energy distribution as shown in Fig. 13.

The Doppler broadening of the X-ray lines $g(\Delta \omega )$ is described by formulas similar to Eqs. (39,40):

$\begin{displaymath} g(\Delta \omega )=\frac{1}{2\xi }\int _{(\Delta \omega /\xi )^{2}}^{E_{max}}\frac{w(E)}{\sqrt{E}}dE \end{displaymath}$

(38)

$\begin{displaymath} \xi =\frac{\omega _{0}}{c}\sqrt{\frac{2}{M}} \end{displaymath}$

(39)

where $\omega _{0}$ is the transition energy. Therefore the same method can in principle be applied for the kinetic energy distribution of the muonic hydrogen from the Doppler profile of the X-ray lines. In this case, however, the limits of the final energy resolution are significant and proper corrections must be applied before using the formulas mentioned above. The extension to the case of pionic hydrogen, where the nuclear reaction widths should be taken into account, is straightforward.

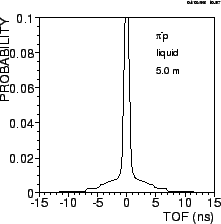
$\resizebox* {0.4\textwidth}{0.2\textheight}{\includegraphics{tof_liq.epsi}}$

Figure 12: The calculated neutron ToF spectrum for the reaction $(\pi ^{-}p)_{at}\rightarrow n+\pi ^{0}$ in liquid hydrogen for a neutron flight path of 5m.

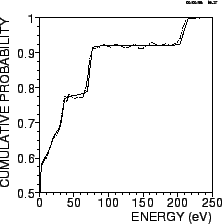
$\resizebox* {0.4\textwidth}{0.2\textheight}{\includegraphics{wec1.epsi}}$

Figure 13: The cumulative energy distribution W(E) reconstructed from the nToF spectrum with $10^{5}$ events (dotted line) in comparison with the exact result corresponding to Fig 11.