



Next: List of Tables
Up: Proposal for an experiment
Previous: Appendix 2: Determination of
Contents
- The calculated spectrum of the kinetic energy of the muonic hydrogen
atom at the instant of the
 transition.
The pressure is
transition.
The pressure is  , the total number of
, the total number of
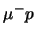 atoms is
atoms is
 .
.
- The calculated spectrum of the kinetic energy of the muonic hydrogen
atom at the instant of the
 transition.
The pressure is
transition.
The pressure is  , the total number of
, the total number of
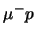 atoms is
atoms is
 .
.
- The calculated spectrum of the kinetic energy of the pionic hydrogen
atom at the instant of the
 transition.
The pressure is
transition.
The pressure is  , the total number of
, the total number of
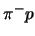 atoms is
atoms is
 .
.
- The calculated spectrum of the kinetic energy of the pionic hydrogen
atom at the instant of the
 transition.
The pressure is
transition.
The pressure is  , the total number of
, the total number of
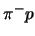 atoms is
atoms is
 .
.
- Set-up of the experiment at the
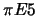 channel at PSI. A very similar set-up will also be used outside the pion area
for the tuning of the spectrometer with X-rays from an ECR-source.
channel at PSI. A very similar set-up will also be used outside the pion area
for the tuning of the spectrometer with X-rays from an ECR-source.
- Pionic deuterium measured with a
 111
spherically bent crystal.
111
spherically bent crystal.
- The intrinsic efficiency of the CCD detector is shown as a function
of energy.
- Simulated spectra for the
 transitions in pionic (left) and muonic hydrogen as measured by a CCD detector
of horizontal width of
transitions in pionic (left) and muonic hydrogen as measured by a CCD detector
of horizontal width of  and a pixel size of
and a pixel size of
 .
The intensity in both lines is 40000. Both lines have a common energy resolution
of
.
The intensity in both lines is 40000. Both lines have a common energy resolution
of
 . A Lorentzian width of
. A Lorentzian width of
 is assumed for the pionic line. The muonic line has a hyperfine splitting of
is assumed for the pionic line. The muonic line has a hyperfine splitting of
 . The distribution of the kinetic energy is as
in Fig. 1 and Fig. 3, respectively. The peak/background ratio for the pionic
line is 100:1.
. The distribution of the kinetic energy is as
in Fig. 1 and Fig. 3, respectively. The peak/background ratio for the pionic
line is 100:1.
- Simulated spectra for the
 transitions in pionic (left) and muonic hydrogen as measured by a CCD detector
of horizontal width of
transitions in pionic (left) and muonic hydrogen as measured by a CCD detector
of horizontal width of  and a pixel size of
and a pixel size of
 .
The intensity in both lines is 40000. Both lines have a common energy resolution
of
.
The intensity in both lines is 40000. Both lines have a common energy resolution
of
 . A Lorentzian width of
. A Lorentzian width of
 is assumed for the pionic line. The muonic line has a 1s hyperfine splitting
of
is assumed for the pionic line. The muonic line has a 1s hyperfine splitting
of
 . The distribution of the kinetic energy is
as in Fig. 2 and Fig. 4, respectively. The peak/background ratio for the pionic
line is 100:1
. The distribution of the kinetic energy is
as in Fig. 2 and Fig. 4, respectively. The peak/background ratio for the pionic
line is 100:1
- Rowland circle and Bragg angles. The Bragg condition requires
reflection at the boundary of a circle with radius of the Rowland circle. D
and S denote the position of detector and source, respectively. At C the Bragg
crystal is mounted. It has a curvature radius
 around O with
around O with  being the radius of the Rowland circle.
being the radius of the Rowland circle.
- The calculated kinetic energy distribution of the
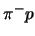 atom at the instant of strong interaction in liquid hydrogen.
atom at the instant of strong interaction in liquid hydrogen.
- The calculated neutron ToF spectrum for the reaction
 in liquid hydrogen for a neutron flight path of 5m.
in liquid hydrogen for a neutron flight path of 5m.
- The cumulative energy distribution W(E) reconstructed from the
nToF spectrum with
 events (dotted line) in comparison
with the exact result corresponding to Fig 11.
events (dotted line) in comparison
with the exact result corresponding to Fig 11.
Pionic Hydrogen Collaboration
1998