Horizontal focussing.

Next: Vertical focussing. Up: Some basic facts. Previous: Some basic facts. Contents

Horizontal focussing.

In the following some expressions for the Johann geometry ( $R_{c}=2\cdot R$ ) with symmetrically cut crystals are given.

The focussing condition for a Johann spectrometer yields for the distances of the source from the crystal SC or detector from the crystal DC:

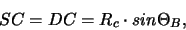$\begin{displaymath} SC=DC=R_{c}\cdot sin\Theta _{B}, \end{displaymath}$

(12)

The distance from the detector ( source) to the origin O of the Rowland circle are given by:

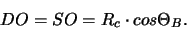$\begin{displaymath} DO=SO=R_{c}\cdot cos\Theta _{B}. \end{displaymath}$

(13)

The distance between detector and source is then given by:

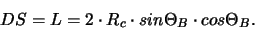$\begin{displaymath} DS=L=2\cdot R_{c}\cdot sin\Theta _{B}\cdot cos\Theta _{B}. \end{displaymath}$

(14)

The detector surface is assumed to be perpendicular to the incident X-rays i.e. perpendicular to CD. The orientation in direction of DO is denoted as x with

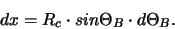$\begin{displaymath} dx=R_{c}\cdot sin\Theta _{B}\cdot d\Theta _{B}. \end{displaymath}$

(15)

With the expression for the angular dispersion given above we immediately get

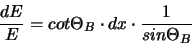$\begin{displaymath} \frac{dE}{E}=cot\Theta _{B}\cdot dx\cdot \frac{1}{sin\Theta _{B}} \end{displaymath}$

(16)

and from this the expression for the dispersion of the crystal:

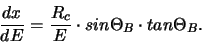$\begin{displaymath} \frac{dx}{dE}=\frac{R_{c}}{E}\cdot sin\Theta _{B}\cdot tan\Theta _{B}. \end{displaymath}$

(17)

Next: Vertical focussing. Up: Some basic facts. Previous: Some basic facts. Contents

Pionic Hydrogen Collaboration
1998