Some basic facts.

Next: Horizontal focussing. Up: Appendix 1: Useful formulae Previous: Appendix 1: Useful formulae Contents

Some basic facts.

The scattering of X-rays of wavelength $\lambda$ on crystal planes with a spacing d is described by the Bragg reflection condition

$\begin{displaymath} n\cdot \lambda =2\cdot d\cdot sin\Theta _{B} \end{displaymath}$

(10)

with n being the order of reflection and $\Theta _{B}$ is the Bragg reflection angle. Differentiation immediately leads to an expression for the local change of the wave length with the Bragg angle $\Theta _{B}$ :

$\begin{displaymath} \frac{d\lambda }{\lambda }=cot\Theta _{B}\cdot d\Theta _{B} \end{displaymath}$

(11)

With $d\Theta _{B}$ replaced by the intrinsic resolution $\omega$ of a crystal ) the resolving power $\frac{\lambda }{d\lambda }$ at the Bragg angle $\Theta _{B}$ is obtained. The need to stay at reasonably high Bragg angles is obvious.

The method of Bragg reflection for energy analysis is based on the extreme angular sensitivity. Values of several $10^{-4}rad$ for $\omega$ are typical for the crystals used in the present experiment. With flat crystals, however, in general only a small part of the crystal surface fulfills the Bragg condition. In the case of the present experiment with a typical distance of $2000mm$ between X-ray source and Bragg crystal only a stripe with a width of a little less than a $mm$ would be usable for one wavelength. In order to reach a higher rate of the X-rays the crystals are bent to an appropriate curvature. For the moment we consider only horizontal cylindrical bending of a crystal whose deflection planes are parallel to the surface (``symmetrically cut crystals'').

The use of bent crystals has long be delayed as a conceptional difficulty arises because of the geometrical impossibility to satisfy simultaneously the two requirements implicit to the Bragg law. These two conditions are:

at all points of the surface the incidence and reflection angles must be the same as referred to the reflection planes ( condition of specular reflection).
at all points of the surface the deflection angle of the beam must be constant in order to obey the Bragg law.

Both Bragg condition and the condition for specular reflection are illustrated in Fig 10. The condition of specular reflection requires that source and detector being on the Rowland circle and the reflecting crystal planes are bent with a radius equal to the diameter of the Rowland circle and being tangential to the Rowland circle in one point. The Bragg law requires the angle of deflection being independent of the deflection point. Both conditions meet only for symmetrical reflection at point C.

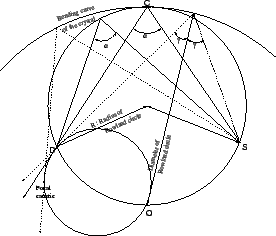
$\resizebox* {0.5\textwidth}{!}{\includegraphics{row.eps}}$

Figure 10: Rowland circle and Bragg angles. The Bragg condition requires reflection at the boundary of a circle with radius of the Rowland circle. D and S denote the position of detector and source, respectively. At C the Bragg crystal is mounted. It has a curvature radius $R_{c}=2\cdot R$ around O with $R$ being the radius of the Rowland circle.

While the conditions 1. and 2. cannot be simulteneously satisfied exactly, they can be satisfied approximately at the cost of aberration. Bending the crystal with $R_{c}=2\cdot R$ ( $R$ being the Rowland radius) as proposed by H. H. Johann [70] leads to a geometrical aberration which depends on the finite width of the crystal. The broadening can still be tolerated as long as the contribution of the geometrical aberration is smaller than the intrinsic resolution of the crystals. This is the case for small enough crystals as used in the present experiment.

It should be mentioned that T. Johannson [88] proposed to grind the surface of a crystal bent to a radius $R_{c}=2\cdot R$ with a grinding radius $R$ . In this way, the crystal surface is tangent to the Rowland circle and the reflecting planes still lie on a cylinder with radius $R_{c}=2\cdot R$ . In the plane the Johannson geometry fulfills the focussing conditions independent of the extension of the crystal. The machining difficulties of such a procedure are tremendous.

Subsections

Next: Horizontal focussing. Up: Appendix 1: Useful formulae Previous: Appendix 1: Useful formulae Contents

Pionic Hydrogen Collaboration
1998