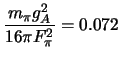Next: Electromagnetic corrections.
Up: Strong interaction
Previous: Scattering length
Contents
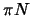 coupling constant
coupling constant
Another motivation for a better direct determination of the pion-nucleon scattering
lengths is connected to the 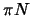 coupling constant
coupling constant 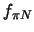 . The Goldberger-Miyazawa-Oehme
(GMO) sum rule [18], which is obtained from a forward dispersion relation
for the isospin-odd
. The Goldberger-Miyazawa-Oehme
(GMO) sum rule [18], which is obtained from a forward dispersion relation
for the isospin-odd 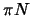 scattering amplitude, provides a relation between
the scattering length
scattering amplitude, provides a relation between
the scattering length 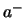 and the
and the 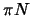 coupling constant
coupling constant 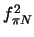 :
:
Here 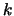 and
and 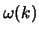 are the incident pion momentum and energy, and
are the incident pion momentum and energy, and
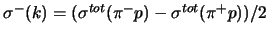 is the isospin-odd total cross section. The integral (5) is known with
an accuracy of the order of 1% (see [36,37,38] and references therein).
Therefore the determination of the width
is the isospin-odd total cross section. The integral (5) is known with
an accuracy of the order of 1% (see [36,37,38] and references therein).
Therefore the determination of the width
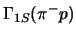 with one percent
accuracy offers the possibility to determine the pion-nucleon coupling with
an accuracy of better than 1%. An immediate application is an evaluation of
the Goldberger-Treiman discrepancy [39,40] which accounts for a small
correction to the Goldberger-Treiman relation
with one percent
accuracy offers the possibility to determine the pion-nucleon coupling with
an accuracy of better than 1%. An immediate application is an evaluation of
the Goldberger-Treiman discrepancy [39,40] which accounts for a small
correction to the Goldberger-Treiman relation
where 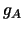 is the axial-vector coupling constant and
is the axial-vector coupling constant and 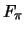 is the weak
pion decay constant.
is the weak
pion decay constant.




Next: Electromagnetic corrections.
Up: Strong interaction
Previous: Scattering length
Contents
Pionic Hydrogen Collaboration
1998
![]() coupling constant
coupling constant ![]() . The Goldberger-Miyazawa-Oehme
(GMO) sum rule [18], which is obtained from a forward dispersion relation
for the isospin-odd
. The Goldberger-Miyazawa-Oehme
(GMO) sum rule [18], which is obtained from a forward dispersion relation
for the isospin-odd ![]() scattering amplitude, provides a relation between
the scattering length
scattering amplitude, provides a relation between
the scattering length ![]() and the
and the ![]() coupling constant
coupling constant ![]() :
: