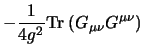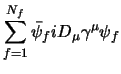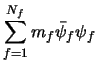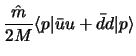Next: Scattering length
Up: Strong interaction
Previous: Strong interaction
Contents
QCD and chiral perturbation theory
The QCD Lagrangian has the form
where 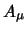 is the gluon field,
is the gluon field, 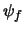 is the quark field of the
is the quark field of the 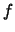 -th flavor
(
-th flavor
(
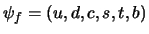 ),
), 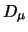 is the covariant derivative,
is the covariant derivative, 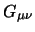 is the field strength tensor, and
is the field strength tensor, and 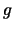 is the
color charge. The term
is the
color charge. The term 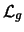 describes pure gluon dynamics, the term
describes pure gluon dynamics, the term 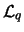 corresponds to the quark
kinetic energy and quark-gluon interaction, and the term
corresponds to the quark
kinetic energy and quark-gluon interaction, and the term 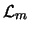 is responsible for the quark masses. In the massless
limit, the QCD Lagrangian
is responsible for the quark masses. In the massless
limit, the QCD Lagrangian
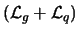 depends on only one dimensionless parameter
depends on only one dimensionless parameter 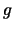 . At the same time
the strong coupling constant
. At the same time
the strong coupling constant 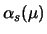 becomes scale dependent due to renormalization. The scale parameter of QCD is
determined from experiment. Provided the quarks are massless, the chirality (helicity) of a quark is conserved and the QCD
Lagrangian is symmetric with respect to rotations in the flavor space independently for
right- and left-handed quarks, thus the massless QCD has the global symmetry
described by the group
becomes scale dependent due to renormalization. The scale parameter of QCD is
determined from experiment. Provided the quarks are massless, the chirality (helicity) of a quark is conserved and the QCD
Lagrangian is symmetric with respect to rotations in the flavor space independently for
right- and left-handed quarks, thus the massless QCD has the global symmetry
described by the group
 . While the Lagrangian
is chirally symmetric, the ground state of the massless QCD (vacuum) does not
have the same property because the chiral symmetry is spontaneously broken:
The characteristic feature of this spontaneous symmetry breaking is the emergence
of massless pseudoscalar particles (Goldstone bosons) (in the case of two flavors,
. While the Lagrangian
is chirally symmetric, the ground state of the massless QCD (vacuum) does not
have the same property because the chiral symmetry is spontaneously broken:
The characteristic feature of this spontaneous symmetry breaking is the emergence
of massless pseudoscalar particles (Goldstone bosons) (in the case of two flavors, 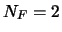 ,
they correspond to the triplet of pions). The essence of the chiral perturbation
theory is to consider the quark mass term
,
they correspond to the triplet of pions). The essence of the chiral perturbation
theory is to consider the quark mass term 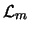 as a perturbation [13].
The mass term explicitly breaks the chiral symmetry, so that the Goldstone bosons
get nonzero masses, and in the leading order the pion mass squared is proportional
to the quark mass: Chiral perturbation theory (CHPT) is an effective field theory constructed
as an expansion in momenta and masses of physical particles, which are considered
to be small on a hadronic scale of about 1 GeV. This approach is extended in
baryon chiral perturbation theory, so that the meson interaction with "heavy"
baryons can be treated as well [12]. Along this way the current algebra
derived long time ago gets a modern framework. The near-threshold pion-nucleon
scattering amplitude is of great interest for chiral perturbation theory. In
particular, the isospin-even part of the
as a perturbation [13].
The mass term explicitly breaks the chiral symmetry, so that the Goldstone bosons
get nonzero masses, and in the leading order the pion mass squared is proportional
to the quark mass: Chiral perturbation theory (CHPT) is an effective field theory constructed
as an expansion in momenta and masses of physical particles, which are considered
to be small on a hadronic scale of about 1 GeV. This approach is extended in
baryon chiral perturbation theory, so that the meson interaction with "heavy"
baryons can be treated as well [12]. Along this way the current algebra
derived long time ago gets a modern framework. The near-threshold pion-nucleon
scattering amplitude is of great interest for chiral perturbation theory. In
particular, the isospin-even part of the 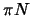 scattering amplitude at the
(unphysical) Cheng-Dashen point (
scattering amplitude at the
(unphysical) Cheng-Dashen point (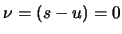 ,
, 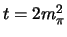 ) is related to
the sigma term which describes the measure of the explicit chiral symmetry breaking:
) is related to
the sigma term which describes the measure of the explicit chiral symmetry breaking:
where 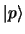 denotes the proton state,
denotes the proton state, 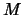 is the proton mass, and
is the proton mass, and
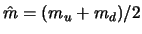 is the average mass of the
is the average mass of the 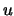 and
and 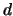 quarks. On the other hand, the sigma
term is related to the observed
quarks. On the other hand, the sigma
term is related to the observed 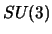 -breaking mass differences in the baryon
octet and the strangeness content of the nucleon. For detailed discussion of
these relations we refer to [11,14,15,16] and references therein.
Since chiral perturbation theory is built as a low-energy expansion, it naturally
concerns low energy parameters, such as scattering lengths and ranges, which
provide very important experimental input determining the parameters of CHPT.
Precise experimental data are therefore crucial for a critical test of the predicting
power of chiral perturbation theory. For a discussion of these topics we refer
to [17] and references therein.
-breaking mass differences in the baryon
octet and the strangeness content of the nucleon. For detailed discussion of
these relations we refer to [11,14,15,16] and references therein.
Since chiral perturbation theory is built as a low-energy expansion, it naturally
concerns low energy parameters, such as scattering lengths and ranges, which
provide very important experimental input determining the parameters of CHPT.
Precise experimental data are therefore crucial for a critical test of the predicting
power of chiral perturbation theory. For a discussion of these topics we refer
to [17] and references therein.




Next: Scattering length
Up: Strong interaction
Previous: Strong interaction
Contents
Pionic Hydrogen Collaboration
1998