The Pion-Nucleon Interaction

The pion-nucleon interaction has been subject both to experimental and theoretical studies since the very beginning of the development of particle physics. On the theoretical side the description of the pion-nucleon system with QCD is considered to be a fundamental issue in the development of this theory. The understanding of strong interaction in the confinement regime has advanced recently, as chiral perturbation theory was developed to perform calculations at low energies [1,2].

Its extension to heavy baryon chiral perturbation theory (HBCHPT) [3] allows to calculate many of the experimentally accessible processes in the meson-nucleon sector. The check of the soundness of this approach requires high precision experiments. This resembles the situation in the development of QED during the last 50 years, where the measurement of the Lamb shift contributed much to the development of QED. In a comparable way the measurement of strong interaction shift and width in pionic hydrogen may be a key experiment in strong interaction physics at low energies.

Pionic hydrogen atoms are produced by stopping negatively charged pions in hydrogen gas. At energies of some eV pions ionize the hydrogen molecule and form an electromagnetically bound system, the so-called pionic hydrogen atom. This atom is dominated by the electromagnetic interaction of its constituents. Their strong interaction is only effective if the wave functions of pions and the proton significantly overlap. In the ground state it results in a broadening of $\approx 1~eV$ and a shift of $\approx 7~eV$ , which has to be compared to an electromagnetic binding energy of $E_{1s}=3238~eV$ . The relations of the measured quantities to the hadronic scattering lengths

describing the $\pi^{-}p\rightarrow\pi^{-}p$ and the $\pi^{-}p \rightarrow\pi^{0}n$ process, respectively, are given by the Deser-type formulae [4,5]:

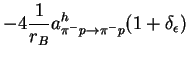$\displaystyle \frac{\epsilon_{1s}}{E_{1s}}$	$\textstyle =$	$\displaystyle -4\frac{1}{r_B} a^{h}_{\pi^{-}p\to\pi^{-}p} (1+\delta_\epsilon)$	(1)
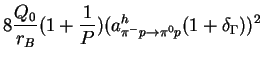$\displaystyle \frac{\Gamma_{1s}}{E_{1s}}$	$\textstyle =$	$\displaystyle 8\frac{Q_0}{r_B} (1+\frac{1}{P}) (a^{h}_{\pi^{-}p\to\pi^{0}p} (1+\delta_{\Gamma}))^2$	(2)

The relations of the measured quantities with the isospin separated scattering lengths $b_{0}$ (isoscalar) and $b_{1}$ (isovector) are given by:

$\begin{displaymath} a^{h}_{\pi^{-}p\rightarrow\pi^{-}p} = b_{0}-b_{1} \end{displaymath}$

(3)

$\begin{displaymath} a^{h}_{\pi^{-}p\rightarrow\pi^{0}p} = \sqrt{2} b_{1} \end{displaymath}$

(4)

The shift and the width of the ground state in pionic hydrogen and deuterium have been determined in a series of experiments of the ETHZ-Neuchâtel-PSI collaboration by measuring the 3-1 transition at 2886 eV with a reflection type crystal spectrometer [10]. An array of 6 cylindrically bent quartz crystals had been used in order to increase the statistics of the experiment. The pions were stopped in a cryogenic target inside a superconducting magnet (cyclotron trap I) and the X-rays were detected with CCD detectors developed at the University of Neuchâtel.

**Figure 1:** Information on $b_{0}$ and $b_{1}$ from scattering experiments and exotic atom data
$\includegraphics [width=.7\textwidth]{b0b1.eps}$

The results improved the value for the strong interaction shift by almost two orders of magnitude compared to earlier work. In addition first results for the width of the ground state were obtained. The error in the width, however, is still almost an order of magnitude bigger than the one in the shift. This excludes the extraction of the isospin separated scattering lengths with errors on the $\%$ -level from the hydrogen experiment alone. The measurement can be useful, however, to put constraints on the different work in phase shift analysis of the scattering experiments in the pion nucleon system.

An illustration of the most recent evaluations for $b_{0}$ and $b_{1}$ from atomic data as well as from scattering data is shown in Figure1. The data from scattering experiments lead to the bands limited by full lines. They have been obtained by critically investigating the different cross sections for the $\pi^{+}p$ (proportional to $b_{0}+b_1$ ), and $\pi^{-}p$ (proportional to $b_{0}-b_1$ ) and charge exchange processes SCX (proportional to

) and extrapolating them to zero energy [11]. All three bands from the different linear combinations of $b_{0}$ and $b_{1}$ coincide in a narrow region in the $(b_{0},b_{1})$ plane with corresponding values of about $b_{1}=-0.082 m_{\pi}^{-1}$ and $b_{0}=0.003 m_{\pi}^{-1}$ each with errors of about $\pm 0.001 m_{\pi}^{-1}$ . As the three different constrains originate from many different sets of experiments, the common intersection can be considered as a quite impressive result. Some criticism was expressed, however, concerning the validity of the model used [12]. It should be mentioned that earlier evaluations of scattering data lead to quite different results [13,14]. Especially the value of $b_{0}+b_{1}$ extracted from the Karlsruhe-Helsinki evaluation with a value of $-0.101 m_{\pi}^{-1}$ contradicts the evaluation mentioned above which assumes $b_{0}+b_{1}=-0.077\pm0.002 m_{\pi}^{-1}$

The data from pionic atoms lead to the regions limited by the dashed lines. As stated before the large error in the width measurement precludes an extraction of $b_{0}$ and $b_{1}$ with sufficient precision. Moreover the band resulting from the shift measurement alone is at variance with the corresponding $\pi^{-}p$ scattering data. A recent evaluation of pionic deuterium shift data results in a small overlapping area if combined with the pionic hydrogen shift data [15]. The results in terms of scattering lengths are $b_{0}=-0.0017\pm0.001 m_{\pi}^{-1}$ and $b_{1}=-0.09\pm0.0012 m_{\pi}^{-1}$ . An evaluation of the ETHZ-PSI-Neuchatel group using earlier theoretical input for the evaluation of the deuterium data resulted in almost the same value for $b_{0}$ but gave a somewhat different value of $b_{1}=-0.0868\pm0.0014 m_{\pi}^{-1}$ [16].

For sake of illustration the dot at $b_{0}=0.0m_{\pi}^{-1}$ and $b_{1}=-0.079m_{\pi}^{-1}$ shows the early current algebra work of Weinberg and Tomozawa [18,19]. A recent HBCHPT calculation to third order expresses the two scattering lengths as a sum of directly calculated values plus terms which are functions of low energy constants [20]. In an evaluation of the low energy constants different authors extract values $-0.01 m_{\pi}^{-1} \leq b_{0} \leq 0.006 m_{\pi}^{-1}$ and $-0.093m_{\pi}^{-1} \leq b_{1} \leq -0.083 m_{\pi}^{-1}$ [21]. A consistent set of experimental data is needed to fix the values for the low energy constants and to check the predictive power of the theory.

A precise measurement of the width is important from a different viewpoint also: it determines the isovector scattering length directly from which a value of the pion nucleon coupling constant can be extracted via the Goldberger-Miyazawa-Oehme sum rule.

In conclusion it can be stated that the results from scattering data and atom experiments are still contradictory and therefore need further investigation. From the side of the atom experiments it should be clarified whether the shift and the width values of pionic hydrogen and deuterium are true strong interaction effects and are not spoiled by the interaction of the pionic atom with the surrounding molecules. In other words the shift and the width measurements for pionic hydrogen and deuterium should be extrapolated to zero pressure. In a second step state of the art electromagnetic corrections should be applied.